Le modèle d’évaluation des actifs financiers

Les Rentiers

3 février 2022

Difficulté : avancé

Le modèle d’évaluation des actifs financiers, traduction pour « capital asset pricing model » (CAPM) en anglais est un modèle de calcul de rentabilité attendue en fonction du risque encouru très utilisé en investissement financier et introduit dans les années 1960. Souvent utilisé sur les actions, il permet de décrire la relation entre le risque et le rendement attendu de ces actifs.

Définition

La CAPM se calcule selon la formule :

Ou les paramètres sont les suivants :

• E(R_actif) : retour sur investissement espéré.
• R_f : Taux sans risque.
• β_actif : volatilité de la rentabilité de l’actif considéré rapportée à celle du marché.
• E(R_m) – R_f : prime de risque, c’est le surplus de rentabilité exigé par les investisseurs lorsque ces derniers placent leur argent sur le marché plutôt que dans un actif sans risque.

Tout cela n’est pas forcément parlant, prenons donc un exemple fictif : une action a un prix de 100 euros, avec un dividende annuel de 2.5%. Ce titre a un rapport beta de 1.3, ce qui signifie qu’il est plus risqué que le marché. Le taux de risque est de 1% et la progression du marché est estimée à 6% :

On espère donc de cette action un rendement total de 8.15%, cela comprend les dividendes et l’appréciation en capital.

Les limites du CAPM

Le modèle d’évaluation des actifs financiers a été mis au point dans les années 1960, il y a donc plus de 60 ans. Sa formule claire et son calcul simple font qu’il est toujours très utilisé pour comparer diverses opportunités. Bien que le modèle reste théoriquement valide, la réalité en a montré quelques limites :

• Les marchés sont compétitifs et de plus en plus efficaces pour absorber les informations, lesquelles deviennent donc rapidement obsolètes.
• Les marchés sont dominés par des investisseurs rationnels et averses au risque, qui cherchent à maximiser la les retours sur leurs investissements.

D’autres imprécisions se glissent également dans la formule. Par exemple, la présence du beta suppose que le risque peut être mesuré par la volatilité du prix d’une action. Cependant, cette volatilité et son risque induit ne sont pas les mêmes à la hausse ou à la baisse, de même que deux actions ayant le même bêta ne réagiront pas exactement de la même façon à une augmentation de la volatilité. Enfin, la période rétrospective pour la déterminer n’est pas standard, les rendements et le risque n’étant pas normalement distribués au sens mathématique du terme.

La formule suppose également que le taux sans risque restera constant sur la période visée, ce qui ne sera pas le cas dans la réalité. Dans l’exemple précédent, nous avions pris un taux sans risque de 1%, mais rien ne dit que quelques années plus tard le taux de la BCE n’atteigne pas 3%. Une augmentation du taux sans risque augmenterait alors le coût du capital utilisé et ferait mécaniquement monter le rendement relatif de l’action.

Le paramètre nommé marché sera quant à lui souvent pris comme la performance de l’indice de référence telle que le CAC40, ce qui est là encore une approximation.

Enfin, cette formule possède les mêmes travers que l’analyste technique puisqu’elle suppose que les données passées présagent des données futures, ce qui est une assertion fausse en tant que telle.

La frontière d’efficacité

Tâchons de visualiser ce dont nous parlons afin de nous en faire une idée plus précise. Le calcul du retour sur investissement en fonction du risque permet de placer les différents titres analysés sur un graphique :

• En abscisse : le niveau de risque
• En ordonnée : le niveau de retour sur investissement attendu

Se trouve donc la progression linéaire théoriquement parfaite, celle qui relie directement le retour sur investissement au niveau de risque. Cette droite s’appelle la ligne du marché des capitaux, capital market line (CML) en anglais. On peut considérer que par rapport à cette séparation, tout ce qui se trouve au dessus est sous-évalué (en vert), tout ce qui se trouve en dessous surévalué (en rouge).

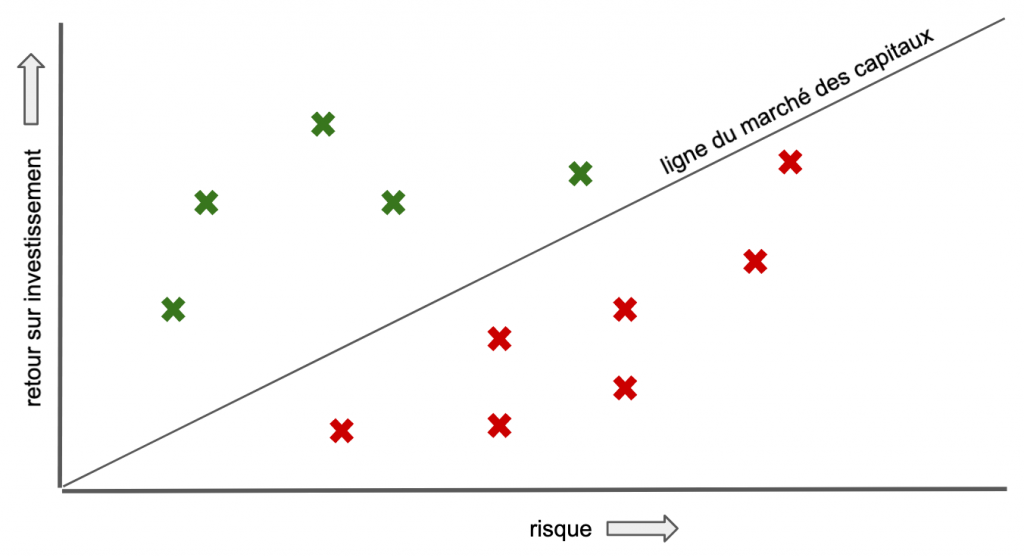
Evidemment, il est difficile de trouver des valeurs du bon côté de la ligne du marché des capitaux. Parmi celles présentes de l’autre côté, la formule dessine une courbe nommée frontière d’efficacité, ou efficient frontier en anglais. C’est souvent elle qui, dans le monde réel, séparera les bons investissements des valeurs plus spéculatives.

Les valeurs dites efficaces sont ainsi représentées en bleu, seules restent en rouge celle se trouvant dans la zone à eviter.

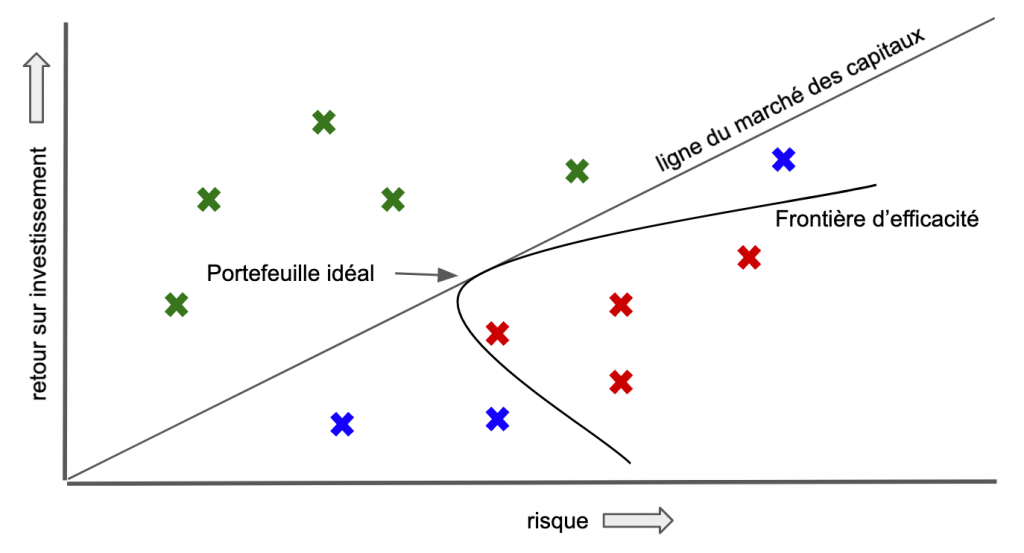
On voit que cette frontière dessine une courbe venant effleurer la ligne de marché des capitaux. En dessous de cette courbe, les valeurs peu risquées mais à faible rendement. Au dessus, la prise de risque supérieur en échange d’un meilleur rendement espéré. Ainsi, le portefeuille idéal entre ce qui est possible de trouver et qui s’avèrera efficace réside à la jonction de ces deux courbes.

La ligne du marché des capitaux et la frontière d’efficacité sont dans la réalité difficiles à définir, mais illustrent un concept important : celui du compromis entre un rendement accru et un risque accru. Parce qu’il est impossible de créer le portefeuille parfait correspondant à la ligne du marché des capitaux, il est courant que les investisseurs prennent trop de risques lors de leur recherche de rendement supplémentaire. Ce graphique peut alors aider à les guider vers des choix plus rationnels.

En conclusion

Le CAPM utilise un modèle mathématique pour déterminer si un titre est évalué à sa juste valeur. Il repose sur des hypothèses de base, sur les distributions de risque et de rendement et les fondamentaux du marché qui sont forcément une représentation idéale de la réalité. Cependant, les concepts sous-jacents du CAPM et la frontière d’efficacité peuvent aider les investisseurs à comprendre la relation entre le risque et le retour sur investissement attendus de leurs décisions d’achat ou de conservation de titres.